With a beam energy of 3.3 MeV, we populate only the ground state of 14N, since the first excited state is just above 2 MeV and the Q value is only +1.2 MeV.
Do kinematic calculation (JRelkin) for forward angles, for 3.3 and 3 MeV beam energy (assuming 300 keV energy loss in gas for the second case). Arbitrarily choose reaction positions of 10 and 8 cm upstream of the detectors. (Pretend the system has cylindrical symmetry for now...add the complication of the real detector geometry later on.) Then see what measured position the real thetas would give, and what information we can glean...
Here's the particle energies vs. the real thetas...
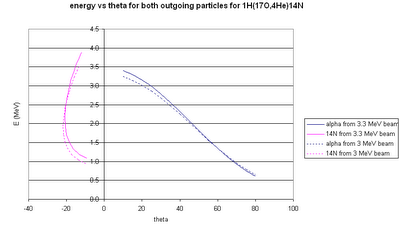
...and the particle energies vs. the measured radial position...
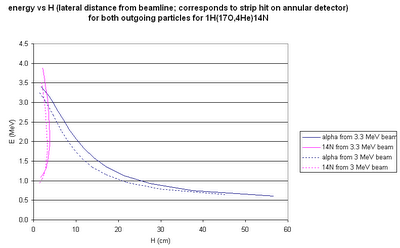
And here's the angular distribution of the outgoing alphas and 14N:
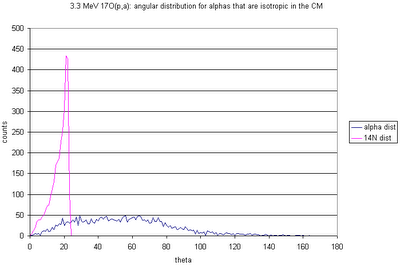
No comments:
Post a Comment