17O (p,α) odds and ends

1. 10 Torr results for reaction...
¹⁴N hits on S2, with some corresponding alpha hits... (I said proton before--I meant alpha!)


...and the remaining corresponding alphas on the "barrel" detectors...


2. 10 Torr: elastic proton rate:
I made a...let's call it a careless oversimplification with the angular distribution for the previous proton rate calculation; but I don't think it had much of an effect. On the other hand, the incorrect number of atoms in the target that I used DID have an effect--the rates I calculated were at least an order of magnitude too high. I did a very detailed new calculation of energy losses for the protons.

The input:
H₂ gas: pressure=10 Torr, total cell length=10 cm
beam: 3.3 MeV ¹⁷O
detectors: S2 and barrel detectors in the now-standard positions
scattering cross-section: calculated by Tom
atoms in target: 7e16 atoms/cm²
beam current: 1e11 pps
protons to damage detector: 1e11 per cm²

The results:
520 000 protons/s in barrel; 970 000 protons/s in S2
--> 5200 protons/cm²/s in barrel; 28 000 protons/cm²/s in S2
--> 1.9e7 s to damage barrel; 3.6e6 s to damage S2
-->445 (12 h) shifts to damage barrel; 83 shifts to damage S2.

If (if) these new calculations are correct, we don't need to worry about limiting beam current to keep from frying the detectors. Also, the rate in a single strip of the S2 would be ~20 000 protons/s (but they could be eliminated by setting a threshold), and there would be a 13% chance of having a proton come in at the same time as a ¹⁴N. Not too bad!

3. Calibration reaction:
Chafa and Fox both use the ¹⁸O + p --> E^lab_R=151 keV ¹⁹F resonance for calibration. As near as I can tell, that level in ¹⁹F has a width Γ>0.3 keV (quite different from the 0.3 eV width of the state of interest in ¹⁸F). That means that the width of the state (instead of the beam energy loss in the gas) becomes the dominant factor in the resonance length in the cell.
Here's the kinematic curves for the reaction...



But because the reaction can happen at any point in the cell (instead of at a nicely constrained point like in the ¹⁷O+p reaction), the measured energy-versus-detector-position curves are smears...note that the x-axis on both of these plots bears no resemblance to the actual extents of the detectors....





At the least this means that the efficiency for detecting this "calibration" resonance will be quite low and hard to determine. Also, particle identification will be hard in the absence of clear loci for the particles of interest--how will we tell them apart from contaminant reactions?

Comments?

26Alm experiment at Yale

Since all of the proton decays that we see are L=0, there's nothing to prevent us from putting the spectrometer at non-zero angles. The disadvantage is that each strip must be treated separately instead of adding strips of the same theta from different detectors together, and this in itself might be enough to require that the spectrometer be at zero degrees...but here's what happens if it isn't:

Ingredients:
30 MeV p beam.
Energy loss and straggling of proton beam and proton decay through a 100 μg/cm² metallic ²⁸Si target.
Tag on d to isolate decays from an 8.5 MeV level in ²⁷Si to the ground, metastable, and second excited states of ²⁶Al.
YLSA in the standard position (assuming all five sectors working!).
Energy loss and straggling of protons through dead layer of YLSA; also assume that YLSA has a resolution of 15 keV for protons.

Results:
Energy (average; error bars represent standard deviation) of protons in each individual strip of YLSA for a spectrometer angle of 0'... (click on a picture for a bigger version)



...and 10'


I was afraid that somehow the spectrometer angle would lead to a blurring of the individual decays' lines, making them harder to resolve; but as long as the strips are treated separately, there should be no problem with resolution.

Comments?

17O(p,α) detector configuration

Ingredients

• beam energy spread of 0.4% (Marco's best estimate)
• gas cell pressure of 4.5 Torr (could increase this)
• 120 mm between beginning of high-pressure region and S2
• "barrel" detectors of lengths, widths, and positions to be determined...
• beam diameter of 3 mm (fwhm) (estimate from Dave H.)
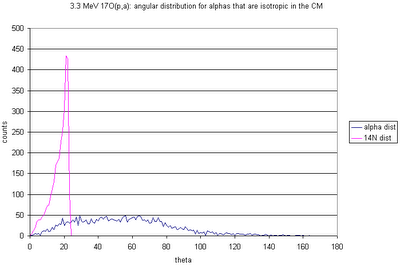
• Breit-Wigner cross section for reaction through 183 keV (cm) resonance with width of 0.3 eV: energy dependence goes as
  1/[(E-E_R)² + (Γ/2)²]
  where Γ is the total width of the excited state in ¹⁸F.
  

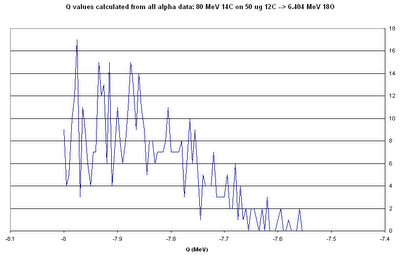
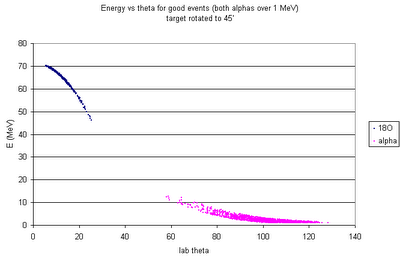
The figure above shows the (renormalized) Breit-Wigner cross-section calculated for each event. (For all figures, click for a larger version.)


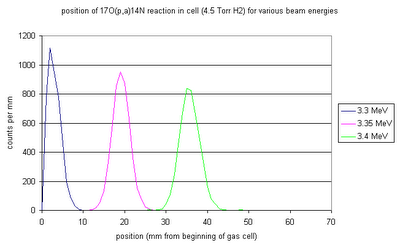
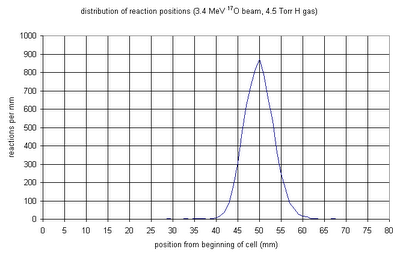
Combining the beam resolution, energy loss/straggling in gas, and the width of the resonance gives the above distributions of reaction positions for various initial beam energies. Higher initial energies move the resonance position downstream in the cell, and as the straggling of the beam through the gas cell becomes more severe the resonance length in the cell increases.

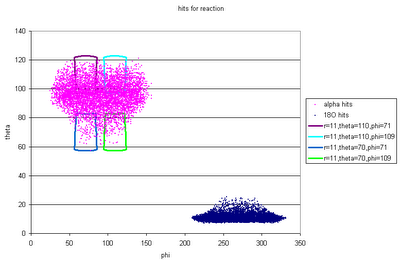
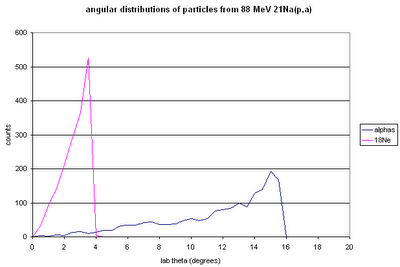
Here are two more figures showing distributions of resonances: the first with respect to position in the cell, and the second with respect to beam energy at that position.





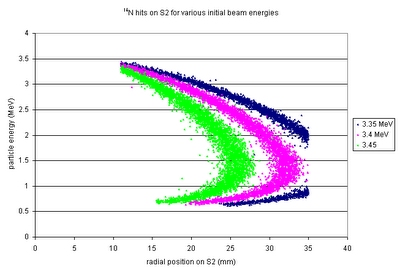
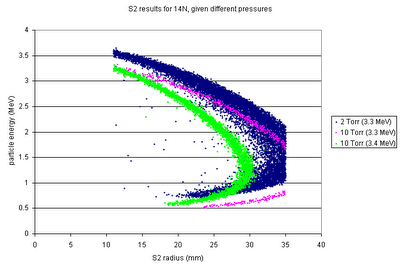
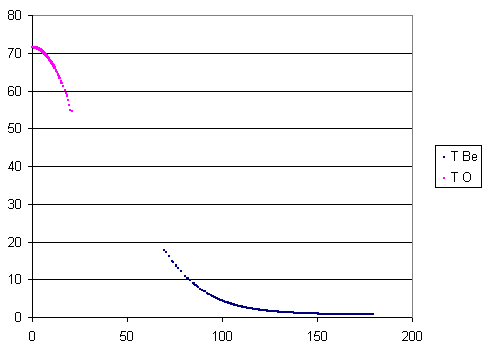
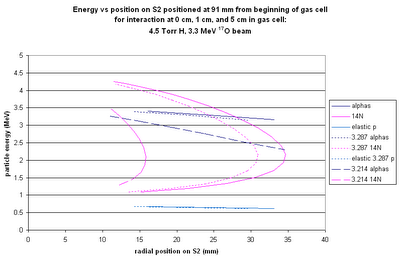
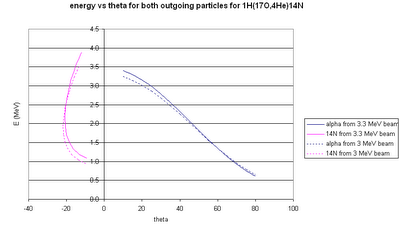
The ¹⁴N from different possible beam energies will have different energy-position curves on the S2.



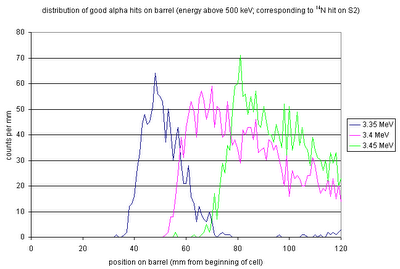
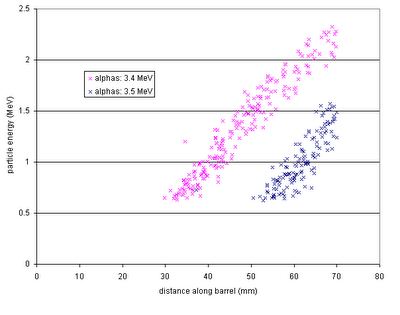
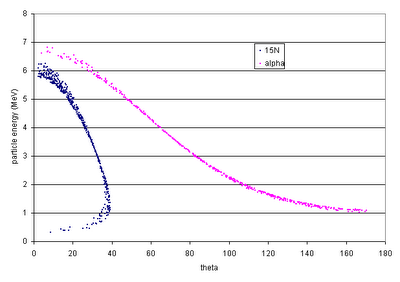
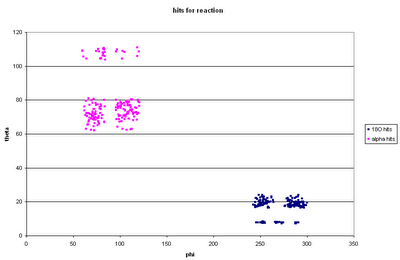
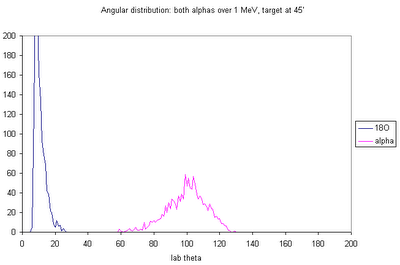
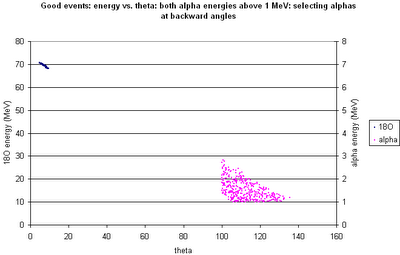
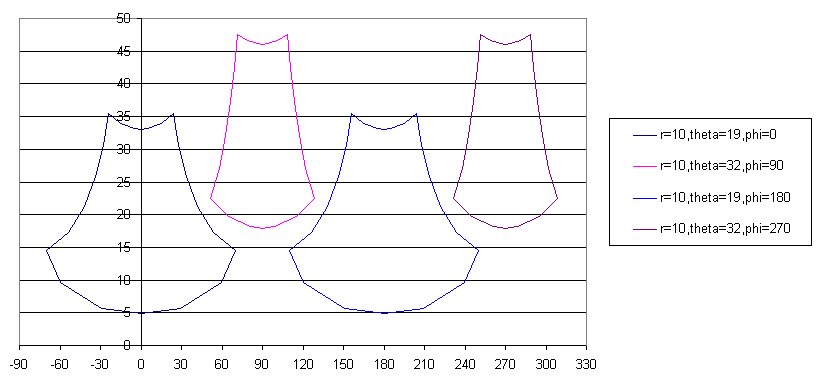
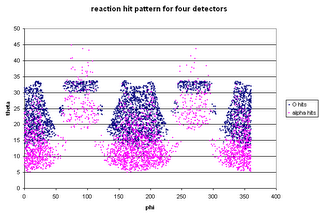
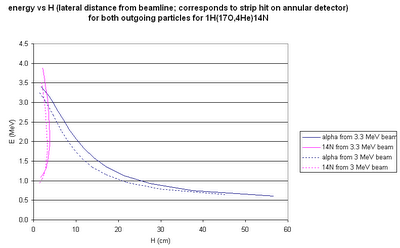
The corresponding alphas (with energies high enough to be detected!) will have the above position distributions on the barrel detectors.

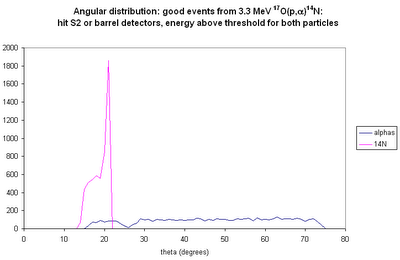
Try the following configuration: four 5 cm x 5 cm double-sided silicon strip detectors, each at a radial distance of 35 mm from the beam line, with the downstream edge of the active area 10 mm upstream from the S2--so they cover 60-110 mm downstream from the beginning of the cell. Then the efficiency (for detecting both ¹⁴N and alpha with energies above 500 keV) is 53% for E(beam)=3.45 MeV and 37% for E(beam)=3.4 MeV. If we want only ¹⁴N, the efficiencies for those beam energies are 85% and 88% respectively.



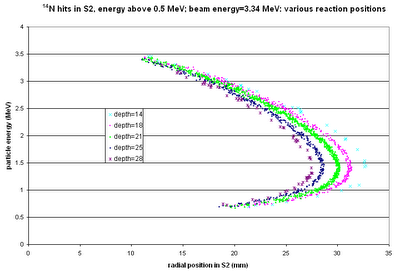
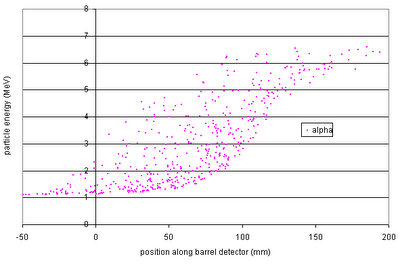
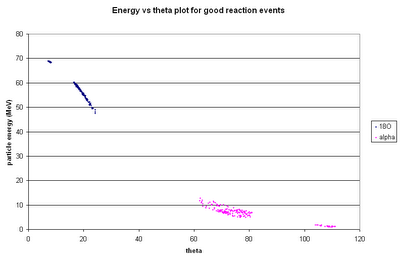
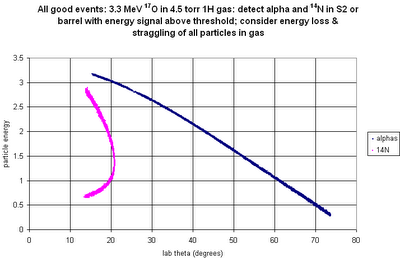
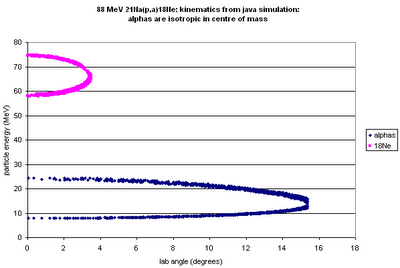
The above shows the kinematic curves for ¹⁴N from reactions at various positions in the cell ("depth=18" --> the reaction position is 18 mm downstream from the start of the gas cell). For the largest-angle events, we could get quite good position resolution, but for smaller angles all the positions blur together.

Rate estimates:
Jonty estimates that the Dragon ¹⁷O(p,γ) experiment will have a rate of 2 counts per hour. Factoring out the 45% BGO efficiency and the 50% charge state efficiency, that's a total of 10 total events per hour. The (p,α) /(p,γ) yield ratio is (so far) reported as 750, so we'd get 7407 total events per hour with Jonty's assumed beam current of 10¹¹ particles per second. With our efficiency, that's 6480 ¹⁴N singles or 3700 coincidences per hour. At the same beam current, we'd also get a LOT of protons, especially into the S2: about 400 kHz per strip. At that rate (and current) it would take 50 hours to fry the S2 (where "fry"=1x10¹¹ protons per cm²--is that right, or can they take more?) (NB: this is taking into account the differential cross section for elastic scattering of the protons, and also their energy loss through the gas and dead layer--most of them do in fact stop before they get to the detector.) Since the protons in the S2 are of lower energy than any of the particles of interest, the thresholds on the data acquisition can be set to eliminate them from the data stream; but there's still the risk of pile-up. At 400 kHz, the time between protons (in an individual strip of the S2) is ~2 μs; the same order as the time to read out a good event--so there's a high probability of getting at least one proton at the same time as a good particle, changing the energy measured. Reducing the current to 10¹⁰ particles per second would increase the average time between protons to ~20 μs--more manageable--and would also increase S2's lifetime to 500 hours (42 shifts--also manageable).
UPDATE: Tom points out that the width of the analogue pulse from the shaping amp (taken to be the width at 0.1% of the maximum amplitude) is ~ 6-7 μs, for a 0.5 μs shaping time; and that the busy time for the DAQ while reading an event is ~ 30 μs.
Using Poisson statistics, the probability of NOT having a proton hit a strip while it is forming the pulse for a good ¹⁴N event is: 6% for 10¹¹ pps; 76% for 10¹⁰ pps; 97% for 10⁹ pps.

In the time it takes to fry the S2 (at whatever current), we could expect to see 325 000 singles and 185 000 coincidences. (That's our total count, from all strips of all detectors; the per-strip counts are lower: for example ~6800 ¹⁴N/strip in the S2.

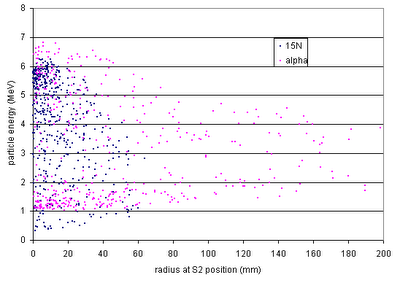
Also: a note about contaminants: Very simple kinematic calculations (no energy loss included) give the following...

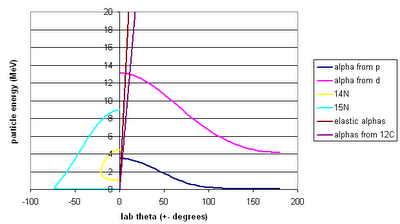
The reactions are on the protons that are supposed to be in the gas cell ("alpha from p", "14N") and on the deuterons ("alpha from d", "15N"), helium ("elastic alphas"), and ¹²C ("alphas from 12C") that might be contaminants in the gas cell. I don't think there's anything to worry about here: the energies are all very different from the energies of the particles we're interested in.

Details about proton rate calculation:

1. Do polynomial fit to elastic scattering cross section calculation:
   
   
   
   
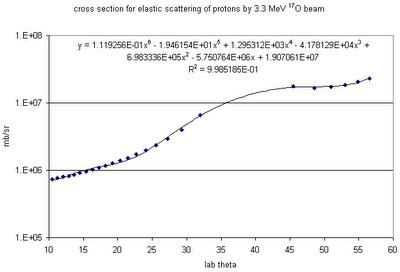
2. Do SRIMulation of energy loss of protons of various initial energies and angles, through the gas and the detector's dead layer; derive fit to fraction of protons that reach detector with energy >1 keV (as function of angle).
   
3. Combine those two fits to give a total probability function: probability of proton of angle θ (and consequently energy E₀) reaching the detector. Apply that probability function to randomly-generated angle in Monte Carlo code.
4. Test the angle to see whether the proton's initial angle and position result in a detector hit.
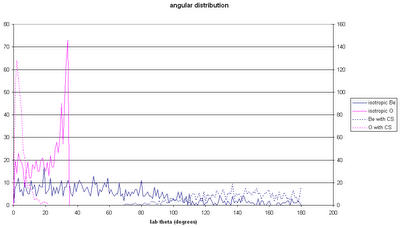
5. Count the total number of detector hits. Renormalize as follows....Use the probability function from step 3; the solid angle for annuli of 1 degree width centred on 10, 11...60 degrees in theta; the atoms/cm2 in the target (2.55e18 for 4.5 torr); the particles per second in the beam; and calculate the total number of particles per second scattered into each 1-degree annulus. Then obtain the same number for the simulation (particles into each annulus for an N-event simulation) and find the renormalization factor that converts (particles per annulus for an N-event simulation) into (particles per annulus per second for a given beam current). Multiply the total number of detector hits by that renormalization factor to get the number of protons per detector per second for the given beam current. The figure below compares the simulation results to the cross section calculation.

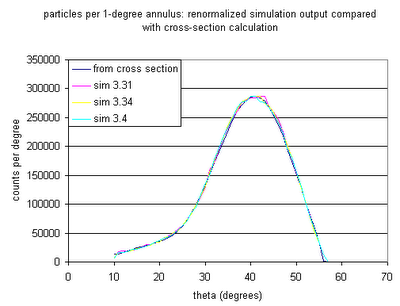
Update:
Alison suggested checking out the effect of different gas pressures. It's fascinating. There are two competing effects that change the length in the cell over which the resonance takes place, as the gas pressure increases: the increased beam energy straggle, and the more abrupt change in beam energy (over length). As it turns out, the straggling is less important, and increasing the gas pressure to 10 Torr could help increase our efficiency or at least make it easier to identify loci:

Orsay: efficiency for our actual detector configuration; also online diagnostics

First step: check that my geometry routine is giving sensible results. Give it the detector locations as input, and see how many randomly-generated directions result in a hit. In this way we can also deduce that the detectors cover 7% of the total solid angle.
Detector locations:
"rd={110,110,110,110,150}
thetad={70,110,70,110,15}
phid={109,109,71,71,270}"



Next step: use the same code (forget about energy loss in the target for now) to see where elastic scattering events hit--both ¹⁴C and ¹²C ejected from target. Just like we see online, most of the ¹⁴C hits are at forward angles in detector 1, and the corresponding ¹²C are in detectors 2 and 4 only.
The thing to note here is that the cross section function used here is purely rutherford--the angular distribution has no "wibbles" in it, to use an Alex-ism.



Now try also reproducing the plots of position in det 1 vs position in det 4: Here we get a smooth curve, whereas online there are two clumps. Either the "wibbles" are making their presence felt, or we're seeing reactions or something in addition to elastic scattering.



Now for reaction: 80 MeV ¹⁴C on 50 μg/cm^{2 12}C: take into account beam spot size, energy loss/straggling in target and dead layer of detector. Hit pattern:



The gaps between the "quad" detectors mean that there are gaps in the "good" ¹⁸O hit pattern in detector 1.

Here's the energy vs. theta plot, too:



Note that both of these "reaction" plots are for good events only, i.e. for events for which the 18O and both alphas are detected and have energies such that the signals at both ends of the strip are above 500 keV. The good events are a small fraction of the total events: 156 total good detector hits for 93180 simulated decays.
10260 O hits; 9825 O hits above threshold
173 alpha hits above threshold
-->0.2% efficiency for good events, although 10.5% efficiency for 18O.

Update: If we move two detectors to 90', we'd get 0.8% efficiency! All we'd have to do is move one mount to 90' on the circular mount, and remove the unused detectors. It would certainly be worth doing this if we're going to run with only two detectors.

Here's the theta and phi ranges of the current quad configuration, together with real 18O hits and potential matching alphas. You can see that most of the potential alphas fall in the gaps between detectors.

Orsay: and now, the bad news

Not to be a total downer or anything...

I've been struggling with my beloved simulations over the past couple of days. I'm not bright enough to figure out exactly why they keep crashing. Crashes notwithstanding, this is my best guess at the distribution of Q values we might expect to get from the resonance we want to populate.

What it includes:
beam spot size, granularity of angles calculated from detector position, all energy losses/straggling and angular straggling in target, energy loss/straggling in detector dead layer, cross section for reaction (correct this time!) with the resulting angular distribution of particles.

What it doesn't include:
any spread in beam energy, whether all particles hit the detectors (I sorta faked the detector effects by assuming all particles go through a dead layer straight-on and have their angular information degraded by a given amount)--so it doesn't give any information about our total efficiency. (this is the part that frustrates me--right now I can't figure out why I can't get the geometric part of the code to work right: it should say whether or not all of the particles hit the detectors and whether the energy signals on both ends are over threshold--but so far it's just crashing. grr.)

With those caveats, this is what the Q value distribution should look like.



Ew. This isn't what we were counting on when we were planning the experiment.

rotated target

Orsay: emergency cross section calculations!

same as above--this time exclude alphas at forward angles: this means that all 18O fall within 5-11'. alphas are really close to the threshold.


angular distribution for isotropic 18O & 8Be, then with the cross section function applied to 18O's cm angle.


...comparing kinematic results from simulation and jrelkin calculation


...and an energy-angle plot for 18O and 8Be, with the cross section applied: to be compared to the plot directly above: all the low-angle 8Be events go away.

17O (p,α) proposal: simulations including energy loss in gas and position of reaction

Here's the results of a simulation that (sort of) takes into account the width of the resonance and the energy loss in the gas.
Assume the reaction takes place within the first centimetre of gas. The S2 is positioned 83 mm downstream from the beginning of the gas cell, and the barrel is cylindrically symmetric at 40 mm from the beamline. The beam has a radius of 1 mm. Energy loss, energy straggling, and angular straggling of the beam before the reaction position are taken into account, using straggling parameters derived from SRIM. The energy loss and straggling of the reaction products through the gas and dead layer are taken into account, but I couldn't figure out how to do the angular straggling through the gas. The dead layer thickness is assumed to be like normal detectors--0.8 μm--but we may end up using thick-deadlayer detectors to compensate for the brightness in the chamber. The energy loss in the deadlayer is significant, particularly for the high-angle protons, so thick deadlayers might actually mean a decrease in efficiency.
what else. I think that's the main parts of the simulation. Here's the results.

E vs. theta for alphas and 14N


angular distributions of just the good events


radius in S2 for both particles for good events


front-back position on the barrel (100 mm is forward, 0 mm is ~100')


Next up: rate calculations, and energy loss simulations for elastically scattered protons.

17O(p,α) proposal: detector positions and efficiency

These are just relkin calculations for 3.3 MeV 17O on a 4.5 Torr H gas target. I make the energy loss over 1 cm of target to be 13 keV. I did the kinematics for the reaction and the elastic scattering at the beginning and end of that range (i.e. 3.3 MeV at 0 cm, 3.287 MeV at 1 cm). The figures are
1. an e vs theta plot: the particle energies (neglecting energy loss/straggling of products in target and in dead layers) vs the real god-given particle angles (again obviously neglecting angular straggling in the target). The lines for the same reaction at the two positions lie practically on top of each other.
2. an e vs S2 position plot. I put an S2 at 91 mm downstream from the 0 cm position, and calculated the radial position of the particles on it, if they hit it. (The position was chosen to maximize the number of 14N we catch: we throw away about 25% of the small-angle 14N with this position, but we'd have to throw away 5% anyway, and it may turn out that this is the optimal position.)
3. an e vs "barrel" position plot. I put a cylindrical barrel of arbitrary length at a radial distance of 40 mm from the beam line, with a starting position somewhere near the S2 (position increases upstream in this plot, so something going off from 0 cm at 90' would be at ~100 mm on the barrel).

Next step: figure out what this means: by detecting the alpha and 14N in some sort of configuration like this, can we deduce the centre of mass energy?

Comment from Tom: putting an S2 inside the dragon gas cell would indeed involve making a new target box. (We're cunning like that.)

A note on efficiency: with an S2 positioned as indicated, we catch 75% of the 14N from the reaction at the 0 cm position. With a 10 cm long cylindrical barrel detector, we catch 82% of the alphas, with an additional 10% going into the S2. The total efficiency is then about 71%. If the barrel detector has less than 100% coverage over its angular range, the efficiency will be decreased by a corresponding amount--for example 50% coverage (like we might get with two rectangular detectors if we were very cunning) leads to 35% total efficiency, whereas with four we might get about 60% total efficiency.

A further note on the figures: the ones I've just uploaded include the effects of reactions at 5 cm as well as at 0 and 1 cm--just to see.

Orsay: detector configuration: reality intervenes

It turned out not to be feasible to use the Deep Space 9 mount after all. Instead, we're going to use the circular mount. Detectors are mounted on L-shaped brackets, which are put at any θ with respect to the beam line (defined from the centre of the detector) and at radial distances ranging from ~10 to ~18 cm. It's easy to mount up to four detectors in plane (i.e. φ=0 or 180), but mounting detectors out of plane will take some work.
That's reality check 1. Reality check 2 is that there just aren't enough amplifiers to go around, if we are planning to use 6 detectors. Stick with 4!
As it happens, the only feasible way to mount 6 detectors on this mount would give us less solid angle and fewer total good events than the best way of mounting four detectors. The best arrangement of four detectors I've come up with has a coverage of 7.5% solid angle, compared with 6.7% for the best feasible arrangement of six detectors.
(Both of these arrangements take into consideration the fact that we can't get closer than 5' or 1.5 cm from the beamline without frying the detectors.)

Here's the outlines of the positions of the four detectors...



...and the reaction hit patterns...



Next up: how we're actually going to mount the detectors in this configuration....

by special request: 21Na(p,α)18Ne

Simple simulation: take 110 or 88 MeV ²¹Na beam energy, 350 μg/cm² CH2 target. Find angular distributions of both α and ¹⁸Ne; what's the detection efficiency with an S2 and another detector (poss. ionization chamber or some sort of silicon)?

I'm assuming isotropic distribution of the alpha particles in the centre of mass. This involves making a very inelegant--but reasonably accurate--transformation from c.m. to lab frames. At some point I'll fix this. Maybe. :-)

I'm also neglecting the effect of the size of the beam spot and all effects of the detectors themselves (energy straggling in the dead layer; granularity of calculated angle due to strip width...)

Here's the kinematic results for the two energies...





and the angular distributions of the particles...





If two S2 detectors are used for the 110 MeV experiment, positioned at 103.4 mm and 333 mm, they catch 1482 of 1834 simulated events (both alpha and 18Ne hit a detector for a given event). 1818 of the 1834 alphas are caught, but only 1482 of the 18Ne: the ones emitted at the smallest angles still escape.

17O (p,α) proposal

Investigating the possibility of putting DSSSDs in the Dragon gas target...will we be able to reconstruct the centre of mass energy from the measured α and ¹⁴N energies and positions?

With a beam energy of 3.3 MeV, we populate only the ground state of ¹⁴N, since the first excited state is just above 2 MeV and the Q value is only +1.2 MeV.

Do kinematic calculation (JRelkin) for forward angles, for 3.3 and 3 MeV beam energy (assuming 300 keV energy loss in gas for the second case). Arbitrarily choose reaction positions of 10 and 8 cm upstream of the detectors. (Pretend the system has cylindrical symmetry for now...add the complication of the real detector geometry later on.) Then see what measured position the real thetas would give, and what information we can glean...

Here's the particle energies vs. the real thetas...



...and the particle energies vs. the measured radial position...



And here's the angular distribution of the outgoing alphas and ¹⁴N:

Orsay: cross sections for various beam energies using FRESCO

I blatantly ripped off Kelly's input file for 14C(12C,8Be): I changed only the order of the target and ejectile parameters in the 7th line--I may have left something out. Assuming that everything's okay, the results are encouraging: the peak of the total cross section is still at a beam energy of 80 MeV.



The angular distribution loooks different now. I don't think Kelly's results had a minimum at 25 MeV, and I also remember there being a couple of orders of magnitude difference between max and min....



Am I doing something wrong?