17O (p,α) proposal: simulations including energy loss in gas and position of reaction

Here's the results of a simulation that (sort of) takes into account the width of the resonance and the energy loss in the gas.
Assume the reaction takes place within the first centimetre of gas. The S2 is positioned 83 mm downstream from the beginning of the gas cell, and the barrel is cylindrically symmetric at 40 mm from the beamline. The beam has a radius of 1 mm. Energy loss, energy straggling, and angular straggling of the beam before the reaction position are taken into account, using straggling parameters derived from SRIM. The energy loss and straggling of the reaction products through the gas and dead layer are taken into account, but I couldn't figure out how to do the angular straggling through the gas. The dead layer thickness is assumed to be like normal detectors--0.8 μm--but we may end up using thick-deadlayer detectors to compensate for the brightness in the chamber. The energy loss in the deadlayer is significant, particularly for the high-angle protons, so thick deadlayers might actually mean a decrease in efficiency.
what else. I think that's the main parts of the simulation. Here's the results.

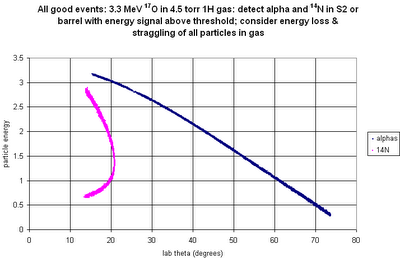
E vs. theta for alphas and 14N


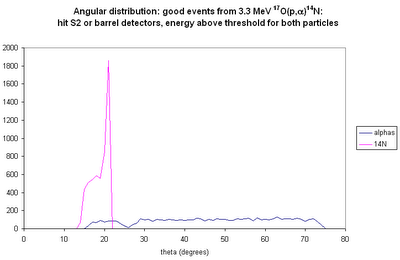
angular distributions of just the good events


radius in S2 for both particles for good events


front-back position on the barrel (100 mm is forward, 0 mm is ~100')


Next up: rate calculations, and energy loss simulations for elastically scattered protons.