17O(p,α) detector configuration

Ingredients

• beam energy spread of 0.4% (Marco's best estimate)
• gas cell pressure of 4.5 Torr (could increase this)
• 120 mm between beginning of high-pressure region and S2
• "barrel" detectors of lengths, widths, and positions to be determined...
• beam diameter of 3 mm (fwhm) (estimate from Dave H.)
• Breit-Wigner cross section for reaction through 183 keV (cm) resonance with width of 0.3 eV: energy dependence goes as
  1/[(E-E_R)² + (Γ/2)²]
  where Γ is the total width of the excited state in ¹⁸F.
  

The figure above shows the (renormalized) Breit-Wigner cross-section calculated for each event. (For all figures, click for a larger version.)


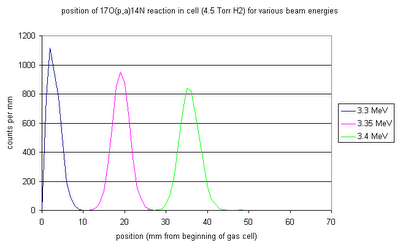
Combining the beam resolution, energy loss/straggling in gas, and the width of the resonance gives the above distributions of reaction positions for various initial beam energies. Higher initial energies move the resonance position downstream in the cell, and as the straggling of the beam through the gas cell becomes more severe the resonance length in the cell increases.

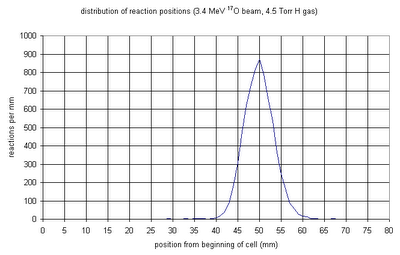
Here are two more figures showing distributions of resonances: the first with respect to position in the cell, and the second with respect to beam energy at that position.





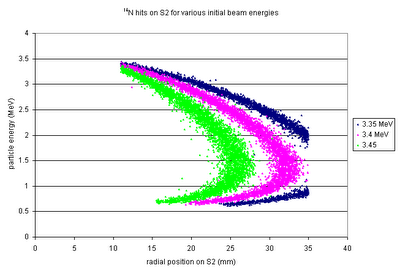
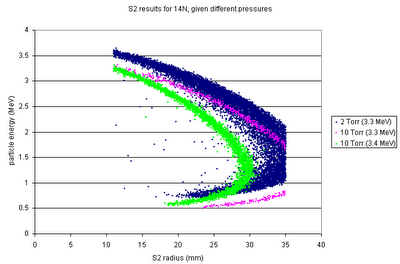
The ¹⁴N from different possible beam energies will have different energy-position curves on the S2.



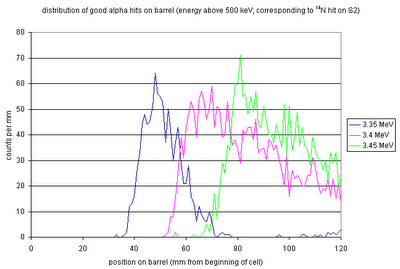
The corresponding alphas (with energies high enough to be detected!) will have the above position distributions on the barrel detectors.

Try the following configuration: four 5 cm x 5 cm double-sided silicon strip detectors, each at a radial distance of 35 mm from the beam line, with the downstream edge of the active area 10 mm upstream from the S2--so they cover 60-110 mm downstream from the beginning of the cell. Then the efficiency (for detecting both ¹⁴N and alpha with energies above 500 keV) is 53% for E(beam)=3.45 MeV and 37% for E(beam)=3.4 MeV. If we want only ¹⁴N, the efficiencies for those beam energies are 85% and 88% respectively.



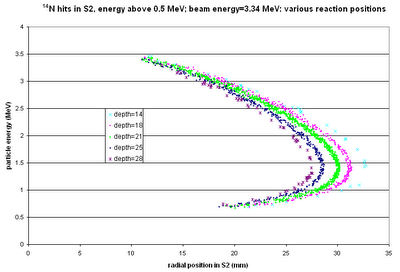
The above shows the kinematic curves for ¹⁴N from reactions at various positions in the cell ("depth=18" --> the reaction position is 18 mm downstream from the start of the gas cell). For the largest-angle events, we could get quite good position resolution, but for smaller angles all the positions blur together.

Rate estimates:
Jonty estimates that the Dragon ¹⁷O(p,γ) experiment will have a rate of 2 counts per hour. Factoring out the 45% BGO efficiency and the 50% charge state efficiency, that's a total of 10 total events per hour. The (p,α) /(p,γ) yield ratio is (so far) reported as 750, so we'd get 7407 total events per hour with Jonty's assumed beam current of 10¹¹ particles per second. With our efficiency, that's 6480 ¹⁴N singles or 3700 coincidences per hour. At the same beam current, we'd also get a LOT of protons, especially into the S2: about 400 kHz per strip. At that rate (and current) it would take 50 hours to fry the S2 (where "fry"=1x10¹¹ protons per cm²--is that right, or can they take more?) (NB: this is taking into account the differential cross section for elastic scattering of the protons, and also their energy loss through the gas and dead layer--most of them do in fact stop before they get to the detector.) Since the protons in the S2 are of lower energy than any of the particles of interest, the thresholds on the data acquisition can be set to eliminate them from the data stream; but there's still the risk of pile-up. At 400 kHz, the time between protons (in an individual strip of the S2) is ~2 μs; the same order as the time to read out a good event--so there's a high probability of getting at least one proton at the same time as a good particle, changing the energy measured. Reducing the current to 10¹⁰ particles per second would increase the average time between protons to ~20 μs--more manageable--and would also increase S2's lifetime to 500 hours (42 shifts--also manageable).
UPDATE: Tom points out that the width of the analogue pulse from the shaping amp (taken to be the width at 0.1% of the maximum amplitude) is ~ 6-7 μs, for a 0.5 μs shaping time; and that the busy time for the DAQ while reading an event is ~ 30 μs.
Using Poisson statistics, the probability of NOT having a proton hit a strip while it is forming the pulse for a good ¹⁴N event is: 6% for 10¹¹ pps; 76% for 10¹⁰ pps; 97% for 10⁹ pps.

In the time it takes to fry the S2 (at whatever current), we could expect to see 325 000 singles and 185 000 coincidences. (That's our total count, from all strips of all detectors; the per-strip counts are lower: for example ~6800 ¹⁴N/strip in the S2.

Also: a note about contaminants: Very simple kinematic calculations (no energy loss included) give the following...

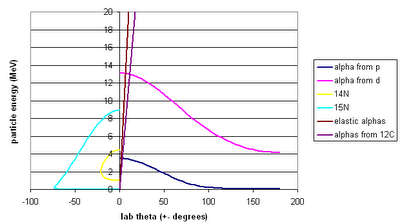
The reactions are on the protons that are supposed to be in the gas cell ("alpha from p", "14N") and on the deuterons ("alpha from d", "15N"), helium ("elastic alphas"), and ¹²C ("alphas from 12C") that might be contaminants in the gas cell. I don't think there's anything to worry about here: the energies are all very different from the energies of the particles we're interested in.

Details about proton rate calculation:

1. Do polynomial fit to elastic scattering cross section calculation:
   
   
   
   
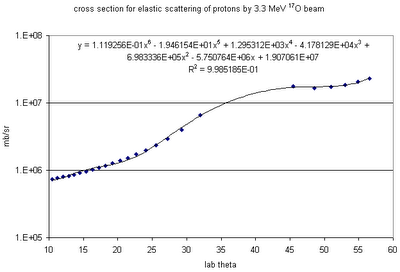
2. Do SRIMulation of energy loss of protons of various initial energies and angles, through the gas and the detector's dead layer; derive fit to fraction of protons that reach detector with energy >1 keV (as function of angle).
   
3. Combine those two fits to give a total probability function: probability of proton of angle θ (and consequently energy E₀) reaching the detector. Apply that probability function to randomly-generated angle in Monte Carlo code.
4. Test the angle to see whether the proton's initial angle and position result in a detector hit.
5. Count the total number of detector hits. Renormalize as follows....Use the probability function from step 3; the solid angle for annuli of 1 degree width centred on 10, 11...60 degrees in theta; the atoms/cm2 in the target (2.55e18 for 4.5 torr); the particles per second in the beam; and calculate the total number of particles per second scattered into each 1-degree annulus. Then obtain the same number for the simulation (particles into each annulus for an N-event simulation) and find the renormalization factor that converts (particles per annulus for an N-event simulation) into (particles per annulus per second for a given beam current). Multiply the total number of detector hits by that renormalization factor to get the number of protons per detector per second for the given beam current. The figure below compares the simulation results to the cross section calculation.

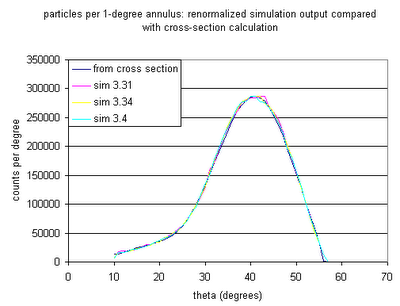
Update:
Alison suggested checking out the effect of different gas pressures. It's fascinating. There are two competing effects that change the length in the cell over which the resonance takes place, as the gas pressure increases: the increased beam energy straggle, and the more abrupt change in beam energy (over length). As it turns out, the straggling is less important, and increasing the gas pressure to 10 Torr could help increase our efficiency or at least make it easier to identify loci: