Orsay: detector configuration: reality intervenes

It turned out not to be feasible to use the Deep Space 9 mount after all. Instead, we're going to use the circular mount. Detectors are mounted on L-shaped brackets, which are put at any θ with respect to the beam line (defined from the centre of the detector) and at radial distances ranging from ~10 to ~18 cm. It's easy to mount up to four detectors in plane (i.e. φ=0 or 180), but mounting detectors out of plane will take some work.
That's reality check 1. Reality check 2 is that there just aren't enough amplifiers to go around, if we are planning to use 6 detectors. Stick with 4!
As it happens, the only feasible way to mount 6 detectors on this mount would give us less solid angle and fewer total good events than the best way of mounting four detectors. The best arrangement of four detectors I've come up with has a coverage of 7.5% solid angle, compared with 6.7% for the best feasible arrangement of six detectors.
(Both of these arrangements take into consideration the fact that we can't get closer than 5' or 1.5 cm from the beamline without frying the detectors.)

Here's the outlines of the positions of the four detectors...



...and the reaction hit patterns...



Next up: how we're actually going to mount the detectors in this configuration....

by special request: 21Na(p,α)18Ne

Simple simulation: take 110 or 88 MeV ²¹Na beam energy, 350 μg/cm² CH2 target. Find angular distributions of both α and ¹⁸Ne; what's the detection efficiency with an S2 and another detector (poss. ionization chamber or some sort of silicon)?

I'm assuming isotropic distribution of the alpha particles in the centre of mass. This involves making a very inelegant--but reasonably accurate--transformation from c.m. to lab frames. At some point I'll fix this. Maybe. :-)

I'm also neglecting the effect of the size of the beam spot and all effects of the detectors themselves (energy straggling in the dead layer; granularity of calculated angle due to strip width...)

Here's the kinematic results for the two energies...





and the angular distributions of the particles...





If two S2 detectors are used for the 110 MeV experiment, positioned at 103.4 mm and 333 mm, they catch 1482 of 1834 simulated events (both alpha and 18Ne hit a detector for a given event). 1818 of the 1834 alphas are caught, but only 1482 of the 18Ne: the ones emitted at the smallest angles still escape.

17O (p,α) proposal

Investigating the possibility of putting DSSSDs in the Dragon gas target...will we be able to reconstruct the centre of mass energy from the measured α and ¹⁴N energies and positions?

With a beam energy of 3.3 MeV, we populate only the ground state of ¹⁴N, since the first excited state is just above 2 MeV and the Q value is only +1.2 MeV.

Do kinematic calculation (JRelkin) for forward angles, for 3.3 and 3 MeV beam energy (assuming 300 keV energy loss in gas for the second case). Arbitrarily choose reaction positions of 10 and 8 cm upstream of the detectors. (Pretend the system has cylindrical symmetry for now...add the complication of the real detector geometry later on.) Then see what measured position the real thetas would give, and what information we can glean...

Here's the particle energies vs. the real thetas...



...and the particle energies vs. the measured radial position...



And here's the angular distribution of the outgoing alphas and ¹⁴N:

Orsay: cross sections for various beam energies using FRESCO

I blatantly ripped off Kelly's input file for 14C(12C,8Be): I changed only the order of the target and ejectile parameters in the 7th line--I may have left something out. Assuming that everything's okay, the results are encouraging: the peak of the total cross section is still at a beam energy of 80 MeV.



The angular distribution loooks different now. I don't think Kelly's results had a minimum at 25 MeV, and I also remember there being a couple of orders of magnitude difference between max and min....



Am I doing something wrong?

Orsay: trying to not fry the detectors

so here's the latest version of the configuration: forward in-plane detectors at r = 150 mm and theta = 15'; backward in-plane detectors at r = 130 mm, theta = 37' (phi = 0,180'); out-of-plane detectors at r = 100 mm, theta = 27' (phi=90,270').

I think this is the best we can do: it's simple to add spacers to the Deep Space 9 mount to move four of the detectors forward, and it avoids putting the detectors at angles smaller than 5' where they would meet a speedy death.

The on-axis strips of the forward in-plane detectors will live for 10.4 days, assuming a 2 pnA beam current and 1e9 elastic events to kill them.

Hit pattern for reaction:



and especially for Alex, schematic drawings of the positions:

Orsay: how to predict detector damage?

So here's what I'm doing about cross sections in the elastic scattering simulation:

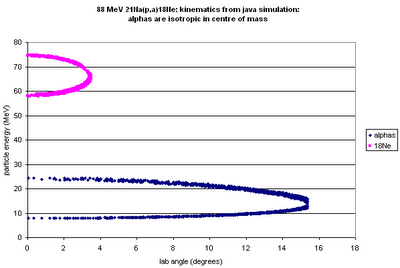
1. Choose a random direction for the outgoing particle (⁸Be).
2. Calculate the c.m. theta corresponding to that direction.
3. Calculate the Rutherford cross section for that angle, normalized to 1 at 5':
   

   double RCS=Math.pow( Math.sin(theta/2) , -4);
   double cross_section=RCS/276237;
   

4. Choose a random number between 0 and 1 ("test").
5. If "cross_section" is greater than "test" then proceed (with energy loss calculations and direction tests and other assorted nonsense); otherwise discard this event and start again.
   

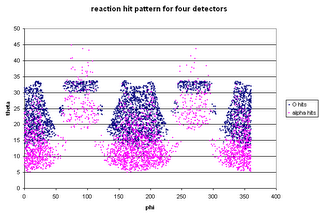
Using this approach I get however-many hits per strip, from elastic scattering, for every however-other-many simulated events.

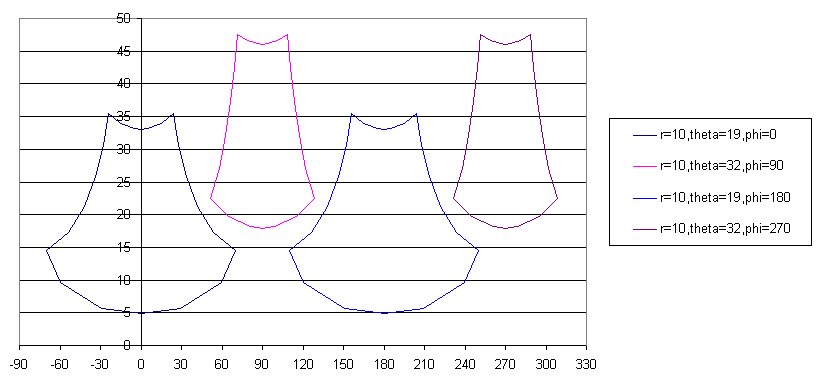
(In a separate calculation, I determined the solid angle for each strip in whatever configuration.)

My question: How do I go from that ratio (and solid angle) to a reasonable estimate of time to damage the detectors?

Other information I have: from Tom's notes:
2.51E+18 atoms/cm2 in target (for 50 ug/cm2 12C target)
1.25E10 particles per second for 2 particle nanoamps
72495.9 mb/sr for elastic scattering at 5'

Someone please tell me how not to be a numpty, and how to combine all this information in a useful way.

Update: I think I might have come up with something.

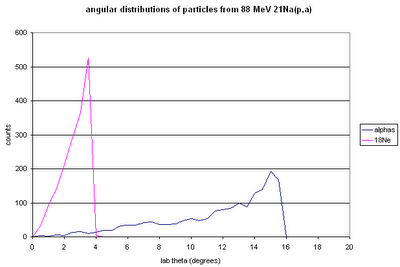
1. Use the Rutherford cross section to calculate the number of events, per second of beam time, into annuli of width 1', centred on 1',2',...55'.
2. Simulate elastic scattering and count how many events go into the same annuli, for a given number of particles on target.
3. Compare the resulting hits-per-degree curves, and find a normalization coefficient that takes us from "simulated hits per X simulated events" to "hits per second".
4. Apply the normalization coefficient to the "hits per strip" calculated above.
5. Deduce the lifetime of each individual strip (i.e. the number of seconds/hours/days for it to get 1e9 hits, with the given beam current).

...I'm too sleepy to go into the gory details right now--maybe tomorrow--but it looks like "configuration 5", my current favourite, will result in the middle half-dozen strips of the detectors that are at lowest angles dying within 5 days. This is good: it gives me another constraint to work with when picking detector positions.

(I figured this out this evening instead of (a) marking the papers I need to hand back first thing tomorrow, (b) working on my Manchester talk, or (c) going to bed early, so maybe I'm still a numpty.)

Orsay: detector configurations AGAIN

I finally got wise and did the high-school geometry necessary to describe the positions of the edges of detectors. Here's what the Deep Space 9 ordinary positions look like...



...and here's my current favourite configuration, affectionately known as "configuration 5"...



For both of these, the legend gives the relevant position information: r, theta and phi values for the centre of each detector.

Here's the hit patterns for elastic scattering (using a Rutherford-esque cross section)...





...and the hit patterns for the reaction...

Orsay: Deep Space 9 mount for PS3Ds

Here's the hit pattern that results from the basic configuration
rd={150,150,150,150,150,150}
thetad={15,37,15,37,27,27}
--that is, all the detectors are at a radial distance of 15 cm; the forward in-plane ones are at theta=15' and the backward in-plane ones have theta=37'; and the out-of-plane detectors are at theta=27'.
In this configuration, there are 1609 hits out of 500 000 events simulated (equivalent to 10477 interactions--so the detectors have an efficiency of 15%.


Modify the configuration: bring the out-of-plane detectors forward by 5 cm.

In this configuration, there are 2093 hits out of 500 000 events simulated (equivalent to 10562 interactions--so the detectors have an efficiency of 20%.

Orsay: energy considerations for S2s

Need to consider whether the particles we want to see will punch through the S2 detectors. Here's the energies of the "good" events with the S2 configuration from below:



Stopping the alphas might be a problem. Here's what SRIM says:...actually the table formatting is too hard to read. Never mind. What it says is that 25 MeV alphas stop in 317 um of Si, and 35 MeV alphas stop in 564 um. Even the Edinburgh 500-micron S2s won't be enough to stop the forward alphas.

(Stopping the Oxygen is not a problem--just a few microns does it.)

Orsay: trying out S2 detectors

Although we don't have LEDAs to burn, we do have S2s, apparently. Try those: at 55 and 190 mm from the target they cover 3.3-32.5' with really high efficiency. The hit pattern is shown below...



...and the angular distribution of ¹⁸O and α hits:


Compare these to the hit patterns and ang dists of one arrangement of 6 ps3ds:




Advantages of using S2s instead of PS3Ds: Lots of coverage; easy analysis; Q value no less precise; fewer channels of electronics; fewer detectors to fry.

Disadvantages: we have to scramble for pre-amps and cabling and such; and we don't get to use the Deep Space Nine mount.

Thoughts?

Orsay: Why are we using position-sensitive strip detectors, again?

...besides the logistical "that's what we have on hand to fry" reasons, I mean--which in themselves can be pretty compelling.

While poking around looking for the best way to arrange the PSSSD detectors (on which more anon), I got to thinking how nice it would be to have something that gave full coverage at small angles. Then I got to thinking, well, maybe we need the extra-good position resolution that the PS3D detectors provide. Then I figured, hey, why not test that assumption. So here's the results: Q calculated for the 6.404 MeV level in ¹⁸O, various different ways: 1. using the true value of θ; 2. using the true values of both θ and φ; 3. using the value of θ that the PS3D gives us; 4. using both θ and φ from the PS3D. (Using θ and φ measured for the alphas you calculate x, y, and z momentum components for the residual nucleus and then use that to calculate its energy and hence Q; using just θ you calculate the parallel (to the beam direction) and perpendicular components of its momentum.)



What you see is that it makes no difference whether you use φ to calculate Q or not. This suggests that the bad φ resolution of LEDA or S2 detectors wouldn't be a problem. Check it out.



When you calculate Q with LEDA/S2 θ information, you get (essentially) the same result as from the PS3Ds, even though if you include φ, the resolution is crap. For comparison, the PS3D θ result is shown on the same plot.

Conclusion: Using concentric-strip detectors in this case doesn't limit the quality of the information we get. There's a chance that it might improve the quantity too. Stay tuned for the next entry...

Orsay: angular distributions for different species

Here's a comparison of alphas and ¹⁸O for Ex(180)=6.404 MeV: the distributions for all emitted particles are shown, together with the good and sub-threshold events for the current detector configuration (config C, shown in an entry below)

Orsay: take out delta-E detectors: resulting Q-value distribution