Orsay: efficiency for our actual detector configuration; also online diagnostics

First step: check that my geometry routine is giving sensible results. Give it the detector locations as input, and see how many randomly-generated directions result in a hit. In this way we can also deduce that the detectors cover 7% of the total solid angle.
Detector locations:
"rd={110,110,110,110,150}
thetad={70,110,70,110,15}
phid={109,109,71,71,270}"



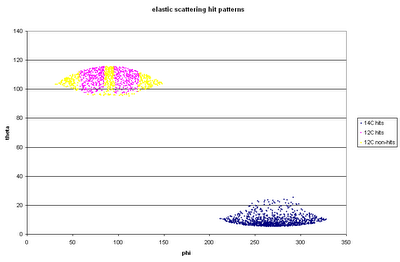
Next step: use the same code (forget about energy loss in the target for now) to see where elastic scattering events hit--both ¹⁴C and ¹²C ejected from target. Just like we see online, most of the ¹⁴C hits are at forward angles in detector 1, and the corresponding ¹²C are in detectors 2 and 4 only.
The thing to note here is that the cross section function used here is purely rutherford--the angular distribution has no "wibbles" in it, to use an Alex-ism.



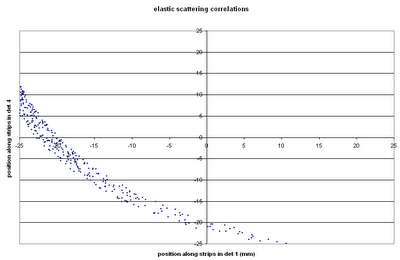
Now try also reproducing the plots of position in det 1 vs position in det 4: Here we get a smooth curve, whereas online there are two clumps. Either the "wibbles" are making their presence felt, or we're seeing reactions or something in addition to elastic scattering.



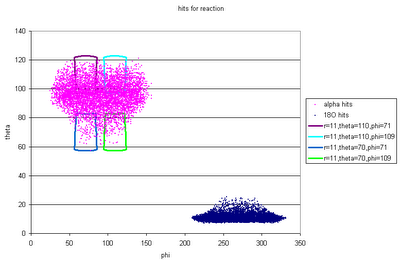
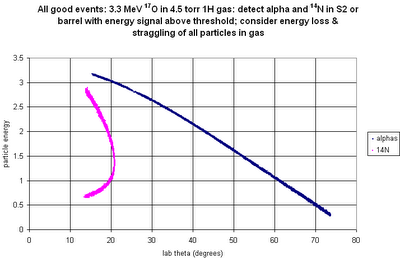
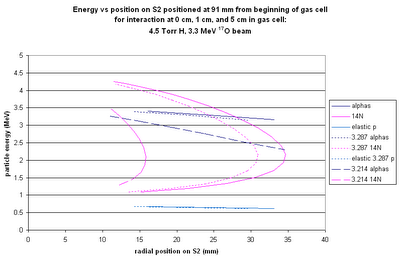
Now for reaction: 80 MeV ¹⁴C on 50 μg/cm^{2 12}C: take into account beam spot size, energy loss/straggling in target and dead layer of detector. Hit pattern:



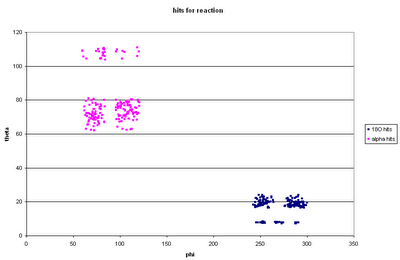
The gaps between the "quad" detectors mean that there are gaps in the "good" ¹⁸O hit pattern in detector 1.

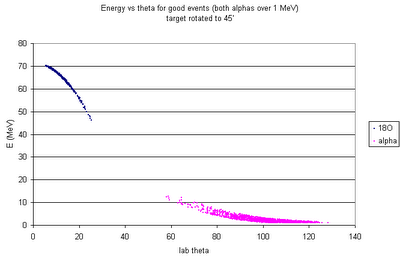
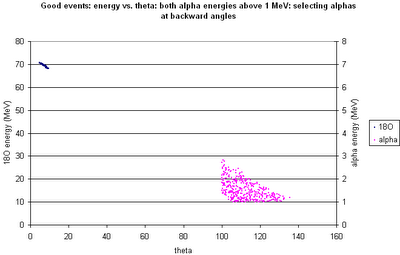
Here's the energy vs. theta plot, too:



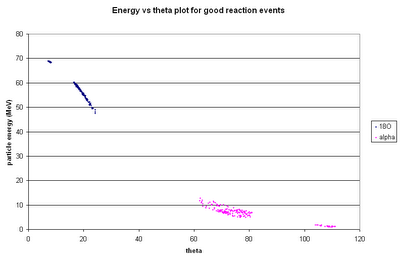
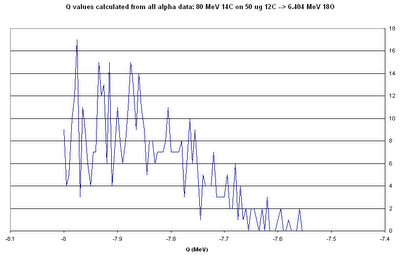
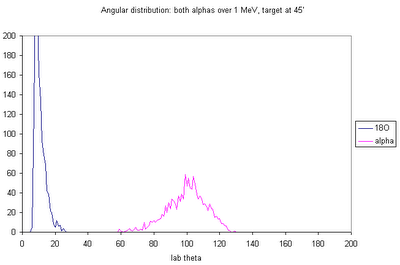
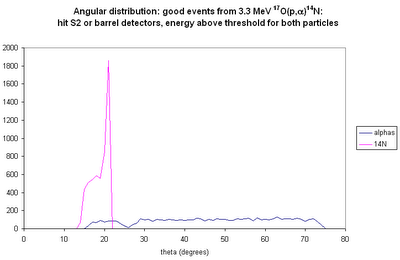
Note that both of these "reaction" plots are for good events only, i.e. for events for which the 18O and both alphas are detected and have energies such that the signals at both ends of the strip are above 500 keV. The good events are a small fraction of the total events: 156 total good detector hits for 93180 simulated decays.
10260 O hits; 9825 O hits above threshold
173 alpha hits above threshold
-->0.2% efficiency for good events, although 10.5% efficiency for 18O.

Update: If we move two detectors to 90', we'd get 0.8% efficiency! All we'd have to do is move one mount to 90' on the circular mount, and remove the unused detectors. It would certainly be worth doing this if we're going to run with only two detectors.

Here's the theta and phi ranges of the current quad configuration, together with real 18O hits and potential matching alphas. You can see that most of the potential alphas fall in the gaps between detectors.

Orsay: and now, the bad news

Not to be a total downer or anything...

I've been struggling with my beloved simulations over the past couple of days. I'm not bright enough to figure out exactly why they keep crashing. Crashes notwithstanding, this is my best guess at the distribution of Q values we might expect to get from the resonance we want to populate.

What it includes:
beam spot size, granularity of angles calculated from detector position, all energy losses/straggling and angular straggling in target, energy loss/straggling in detector dead layer, cross section for reaction (correct this time!) with the resulting angular distribution of particles.

What it doesn't include:
any spread in beam energy, whether all particles hit the detectors (I sorta faked the detector effects by assuming all particles go through a dead layer straight-on and have their angular information degraded by a given amount)--so it doesn't give any information about our total efficiency. (this is the part that frustrates me--right now I can't figure out why I can't get the geometric part of the code to work right: it should say whether or not all of the particles hit the detectors and whether the energy signals on both ends are over threshold--but so far it's just crashing. grr.)

With those caveats, this is what the Q value distribution should look like.



Ew. This isn't what we were counting on when we were planning the experiment.

rotated target

Orsay: emergency cross section calculations!

same as above--this time exclude alphas at forward angles: this means that all 18O fall within 5-11'. alphas are really close to the threshold.


angular distribution for isotropic 18O & 8Be, then with the cross section function applied to 18O's cm angle.


...comparing kinematic results from simulation and jrelkin calculation


...and an energy-angle plot for 18O and 8Be, with the cross section applied: to be compared to the plot directly above: all the low-angle 8Be events go away.

17O (p,α) proposal: simulations including energy loss in gas and position of reaction

Here's the results of a simulation that (sort of) takes into account the width of the resonance and the energy loss in the gas.
Assume the reaction takes place within the first centimetre of gas. The S2 is positioned 83 mm downstream from the beginning of the gas cell, and the barrel is cylindrically symmetric at 40 mm from the beamline. The beam has a radius of 1 mm. Energy loss, energy straggling, and angular straggling of the beam before the reaction position are taken into account, using straggling parameters derived from SRIM. The energy loss and straggling of the reaction products through the gas and dead layer are taken into account, but I couldn't figure out how to do the angular straggling through the gas. The dead layer thickness is assumed to be like normal detectors--0.8 μm--but we may end up using thick-deadlayer detectors to compensate for the brightness in the chamber. The energy loss in the deadlayer is significant, particularly for the high-angle protons, so thick deadlayers might actually mean a decrease in efficiency.
what else. I think that's the main parts of the simulation. Here's the results.

E vs. theta for alphas and 14N


angular distributions of just the good events


radius in S2 for both particles for good events


front-back position on the barrel (100 mm is forward, 0 mm is ~100')


Next up: rate calculations, and energy loss simulations for elastically scattered protons.

17O(p,α) proposal: detector positions and efficiency

These are just relkin calculations for 3.3 MeV 17O on a 4.5 Torr H gas target. I make the energy loss over 1 cm of target to be 13 keV. I did the kinematics for the reaction and the elastic scattering at the beginning and end of that range (i.e. 3.3 MeV at 0 cm, 3.287 MeV at 1 cm). The figures are
1. an e vs theta plot: the particle energies (neglecting energy loss/straggling of products in target and in dead layers) vs the real god-given particle angles (again obviously neglecting angular straggling in the target). The lines for the same reaction at the two positions lie practically on top of each other.
2. an e vs S2 position plot. I put an S2 at 91 mm downstream from the 0 cm position, and calculated the radial position of the particles on it, if they hit it. (The position was chosen to maximize the number of 14N we catch: we throw away about 25% of the small-angle 14N with this position, but we'd have to throw away 5% anyway, and it may turn out that this is the optimal position.)
3. an e vs "barrel" position plot. I put a cylindrical barrel of arbitrary length at a radial distance of 40 mm from the beam line, with a starting position somewhere near the S2 (position increases upstream in this plot, so something going off from 0 cm at 90' would be at ~100 mm on the barrel).

Next step: figure out what this means: by detecting the alpha and 14N in some sort of configuration like this, can we deduce the centre of mass energy?

Comment from Tom: putting an S2 inside the dragon gas cell would indeed involve making a new target box. (We're cunning like that.)

A note on efficiency: with an S2 positioned as indicated, we catch 75% of the 14N from the reaction at the 0 cm position. With a 10 cm long cylindrical barrel detector, we catch 82% of the alphas, with an additional 10% going into the S2. The total efficiency is then about 71%. If the barrel detector has less than 100% coverage over its angular range, the efficiency will be decreased by a corresponding amount--for example 50% coverage (like we might get with two rectangular detectors if we were very cunning) leads to 35% total efficiency, whereas with four we might get about 60% total efficiency.

A further note on the figures: the ones I've just uploaded include the effects of reactions at 5 cm as well as at 0 and 1 cm--just to see.