18F(d,p): various factors affecting resolution

The idea: use an ¹⁸F beam of some energy between 14 and 100 MeV on deuterated polyethylene target of some thickness between 10 and 100 μg/cm²: the reaction is ¹⁸F(d,p)¹⁹F*(α)¹⁵N. Detect either just the protons or all three final particles (p, α, ¹⁵N). Calculate the Q value corresponding to the final energies and deduce the excitation energy of ¹⁹F. See whether we can resolve the 6.497, 6.528 MeV levels. Because of the beam's energy loss and straggling through the target, using the proton's final energy to calculate Q might not give very accurate results, whereas the alpha's energy might be a more precise indicator of ¹⁹F's energy.

The input:

• 90 MeV ¹⁸F beam (corresponds to optimum beam energy of 5 MeV/u)
• 20 μg/cm² DH₂ target
• detectors with arbitrary granularity (i.e. pixel size): take the S2 as a starting point: test the effect of changing the theta (annular) strip pitch from 0.5 mm to 1 mm; test the effect of having 16 or 32 phi (radial) strips.
• energy/angular straggling parameters derived from SRIM

Things I've left out

• energy spread of the beam entering the target
• exact cross section (have assumed isotropic distribution in the centre of mass frame).
  

Test, independently, all the different possible contributions to the final Q resolution:

• energy loss/straggling and angular straggling of beam through the target
• energy and angular straggling of the outgoing particles through the target (assume we can reconstruct the energy perfectly, so count the energy straggling but not the energy loss)
• energy straggling of particles in the detectors
• energy resolution of detectors
• beam spot size
• granularity of detectors

Doing the calculations

• Monte Carlo simulation of reaction
• use relativistic energy/momentum to calculate Q (n.b. this is different from e.g. the LLN experiment, where non-relativistic energy/momentum were good enough)

Results
(click on the image for a larger version)

What the graph shows: the standard deviation of the Q values calculated using each different method.
"Qp" means the Q value calculated using only data from the protons; "Qa15" means that only data from the alpha and ¹⁵N are used; Qcalc means that a complicated bit of algebra is done to eliminate the proton and ¹⁵N energies and to reconstruct the beam energy before the reaction.
the different cases:

• "perfect": no energy losses: Q is calculated using the initial energies/angles of all particles
• "beam in target": the reaction takes place at a randomly chosen depth in the target, and uses the beam's modified energy/angle at that point
• "detector energy resolution": see what effect the detector's resolution has: add a gaussian with 15 keV fwhm to a particle's energy
• "particles in target": calculate energy/angle straggling of outgoing particles through the target
• "particles in deadlayer": calculate energy straggling of particles in the deadlayer: assume that the detector is flat and perpendicular to the beamline
• "particles in deadlayer, incidence angle = 0": same as above, only assume that the particles always hit the detectors square on.
• "beamspot size": assume that the beam has a circular profile, with gaussian shapes in the both x and y directions, with σ=1 mm: calculate the precise position of the particles on the detectors, 500 mm down- and upstream.
  
• "detector granularity (standard)": the detectors have 0.5 mm strip pitch and 32 strips in φ,are of infinite extent, and are located 500 mm down- and upstream: calculate the effective position of the particles on the detectors: i.e. the location of the middle of the pixels that the particles hit.
  
• "detector granularity: 16 phi strips": decrease the number of phi strips
• "detector granularity: strip pitch 1 mm": increase the strip pitch

The clever algebra method, Qcalc, does indeed do a better job than the α+¹⁵N method in accounting for the beam energy loss in the target, but that's about its only strength. In general it is decent when it comes to things that mostly affect particles' energies, but it's very sensitive to the particle's angles, so it can't handle granular detectors: the Q values for the realistic detectors range between positive and negative infinity.
The α+¹⁵N method isn't as bad as Qcalc for the granular-detector cases, but it's still pretty bad.
For Qp, the sizes of the spreads in Q introduced by the various factors are all roughly on the same order. They also all depend on the angle of the protons: in some cases they're stronger at backward angles, and in some cases weaker.

Calculate Qp, using all factors combined, and see what the total angular dependence is.
Input: detectors are perpendicular to the beam line, located at 500 mm from the target, and have 0.5 mm theta strip pitch and 32 phi strips; the beam has σ=1 mm; Q is calculated using (proton energy = initial energy + straggling through target + straggling through dead layer + detector resolution factor) and (proton angle = initial angle + angular straggling through target) and (beam energy = average beam energy half way through the target).
Results: Q value as a function of angle, for the two states of interest...

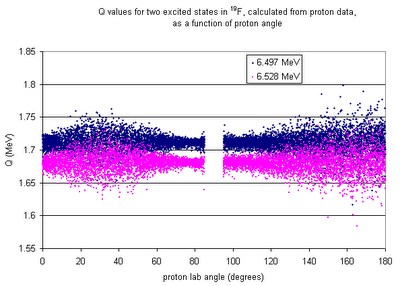
Distribution of Q values for high-angle protons (i.e. theta > 120')

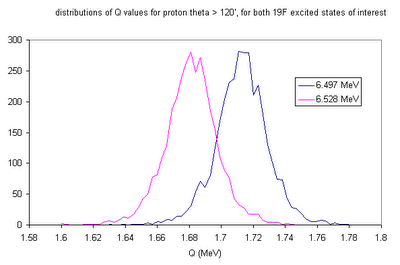
It looks like it's at least possible in theory to make this measurement!